Leetcode 2397 Maximum Rows Covered by Columns Solution in Java | Hindi Coding Community

 

You are given a 0-indexed m x n binary matrix matrix and an integer numSelect, which denotes the number of distinct columns you must select from matrix.

Let us consider s = {c1, c2, ...., cnumSelect} as the set of columns selected by you. A row row is covered by s if:

• For each cell matrix[row][col] (0 <= col <= n - 1) where matrix[row][col] == 1, col is present in s or,
• No cell in row has a value of 1.

You need to choose numSelect columns such that the number of rows that are covered is maximized.

Return the maximum number of rows that can be covered by a set of numSelect columns.

 

Example 1:

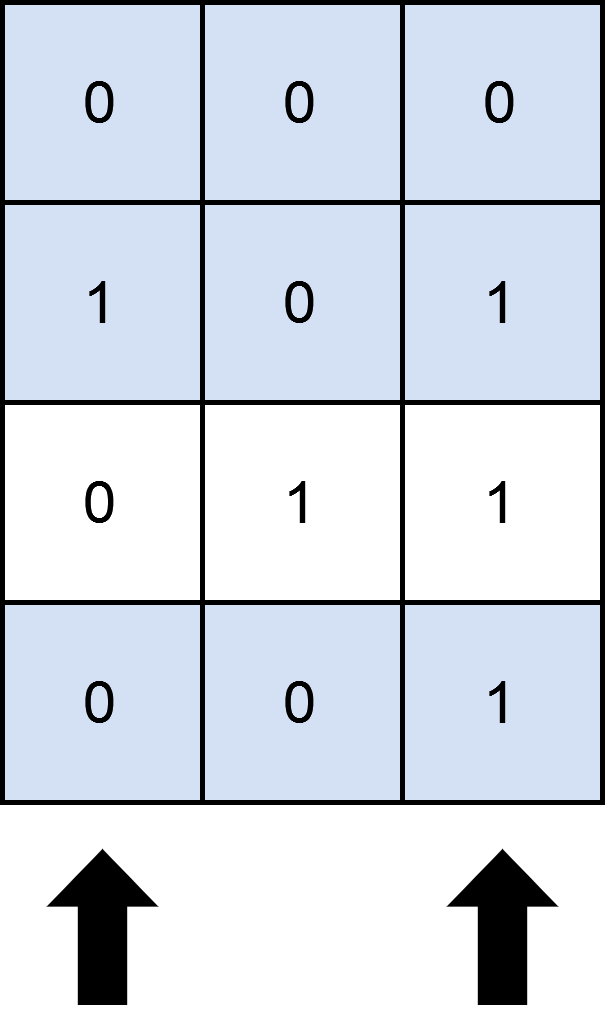
Input: matrix = [[0,0,0],[1,0,1],[0,1,1],[0,0,1]], numSelect = 2
Output: 3
Explanation: One possible way to cover 3 rows is shown in the diagram above.
We choose s = {0, 2}.
- Row 0 is covered because it has no occurrences of 1.
- Row 1 is covered because the columns with value 1, i.e. 0 and 2 are present in s.
- Row 2 is not covered because matrix[2][1] == 1 but 1 is not present in s.
- Row 3 is covered because matrix[2][2] == 1 and 2 is present in s.
Thus, we can cover three rows.
Note that s = {1, 2} will also cover 3 rows, but it can be shown that no more than three rows can be covered.

Example 2:

Input: matrix = [[1],[0]], numSelect = 1
Output: 2
Explanation: Selecting the only column will result in both rows being covered since the entire matrix is selected.
Therefore, we return 2.

 

Constraints:

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 12
• matrix[i][j] is either 0 or 1.
• 1 <= numSelect <= n

Java Code ;

class Solution {

int result;

public int maximumRows(int[][] mat, int cols) {

int m = mat.length; // number of rows

int n = mat[0].length; // number of columns

result = -1;

// if cols is equal to number of columns andswer will be number of rows.

if(cols == n) return m;

// Map to store which column index covers which all rows having value 1.

Map<Integer, Set<Integer>> columnIndexToRowHavingOnes = new HashMap<>();

for(int i = 0; i < n; i++) columnIndexToRowHavingOnes.put(i, new HashSet<>());

for(int i = 0; i < m; i++){

for(int j = 0; j < n; j++){

if(mat[i][j] == 1) {

Set<Integer> set = columnIndexToRowHavingOnes.get(j);

set.add(i);

columnIndexToRowHavingOnes.put(j, set);

}

}

}

getAnswer(0, new ArrayList<Integer>(), cols, columnIndexToRowHavingOnes, m, n);

return result;

}

// Backtracking function

private void getAnswer(int index, ArrayList<Integer> colChoosen, int cols, Map<Integer, Set<Integer>> columnIndexToRowHavingOnes, int m, int n){

// If we have chossed cols number of columns

if(colChoosen.size() == cols){

Set<Integer> rowNotCoveredByChoosenColumns = new HashSet<>();

// For each column

for(int i = 0; i < n; i++){

// find which all rows were missed which have value 1

if(!colChoosen.contains(i)){

rowNotCoveredByChoosenColumns.addAll(columnIndexToRowHavingOnes.get(i));

}

}

result = Math.max(result, m - rowNotCoveredByChoosenColumns.size());

return;

}

if(index == n) return;

// pick the column

colChoosen.add(index);

getAnswer(index + 1, colChoosen, cols, columnIndexToRowHavingOnes, m, n);

// unpick the column

colChoosen.remove(colChoosen.size() - 1);

getAnswer(index + 1, colChoosen, cols, columnIndexToRowHavingOnes, m, n);

}

}