Leetcode 2304 Minimum Path Cost in a Grid Solution in Java | Hindi Coding Community

 

You are given a 0-indexed m x n integer matrix grid consisting of distinct integers from 0 to m * n - 1. You can move in this matrix from a cell to any other cell in the next row. That is, if you are in cell (x, y) such that x < m - 1, you can move to any of the cells (x + 1, 0), (x + 1, 1), ..., (x + 1, n - 1). Note that it is not possible to move from cells in the last row.

Each possible move has a cost given by a 0-indexed 2D array moveCost of size (m * n) x n, where moveCost[i][j] is the cost of moving from a cell with value i to a cell in column j of the next row. The cost of moving from cells in the last row of grid can be ignored.

The cost of a path in grid is the sum of all values of cells visited plus the sum of costs of all the moves made. Return the minimum cost of a path that starts from any cell in the first row and ends at any cell in the last row.

 

Example 1:

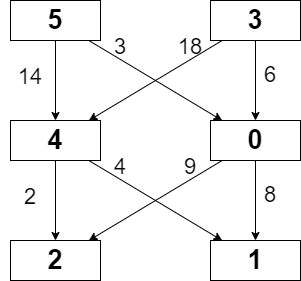
Input: grid = [[5,3],[4,0],[2,1]], moveCost = [[9,8],[1,5],[10,12],[18,6],[2,4],[14,3]]
Output: 17
Explanation: The path with the minimum possible cost is the path 5 -> 0 -> 1.
- The sum of the values of cells visited is 5 + 0 + 1 = 6.
- The cost of moving from 5 to 0 is 3.
- The cost of moving from 0 to 1 is 8.
So the total cost of the path is 6 + 3 + 8 = 17.

Example 2:

Input: grid = [[5,1,2],[4,0,3]], moveCost = [[12,10,15],[20,23,8],[21,7,1],[8,1,13],[9,10,25],[5,3,2]]
Output: 6
Explanation: The path with the minimum possible cost is the path 2 -> 3.
- The sum of the values of cells visited is 2 + 3 = 5.
- The cost of moving from 2 to 3 is 1.
So the total cost of this path is 5 + 1 = 6.

 

Constraints:

• m == grid.length
• n == grid[i].length
• 2 <= m, n <= 50
• grid consists of distinct integers from 0 to m * n - 1.
• moveCost.length == m * n
• moveCost[i].length == n
• 1 <= moveCost[i][j] <= 100

class Solution {

public int minPathCost(int[][] grid, int[][] moveCost) {

int m = grid.length;

int n = grid[0].length;

int[] cost = new int[n];

for(int i = 0; i < n; i++) {

cost[i] = grid[0][i];

}

int ans = Integer.MAX_VALUE;

for(int row = 1; row < m; row++) {

int[] newCost = new int[n];

int tempAns = Integer.MAX_VALUE;

for(int col = 0; col < n; col++) {

int val = Integer.MAX_VALUE;

for(int j = 0; j < n; j++) {

val = Math.min(val, cost[j] + moveCost[grid[row - 1][j]][col]);

}

val += grid[row][col];

tempAns = Math.min(tempAns, val);

newCost[col] = val;

}

cost = newCost;

ans = tempAns;

}

return ans;

}

}