Leetcode 2316 Count Unreachable Pairs of Nodes in an Undirected Graph Solution in c++ | Hindi Coding Community

 

You are given an integer n. There is an undirected graph with n nodes, numbered from 0 to n - 1. You are given a 2D integer array edges where edges[i] = [ai, bi] denotes that there exists an undirected edge connecting nodes ai and bi.

Return the number of pairs of different nodes that are unreachable from each other.

 

Example 1:

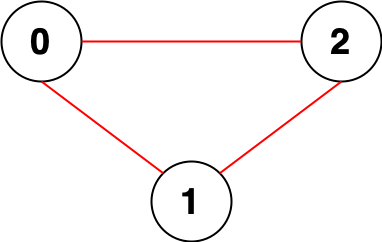
Input: n = 3, edges = [[0,1],[0,2],[1,2]]
Output: 0
Explanation: There are no pairs of nodes that are unreachable from each other. Therefore, we return 0.

Example 2:

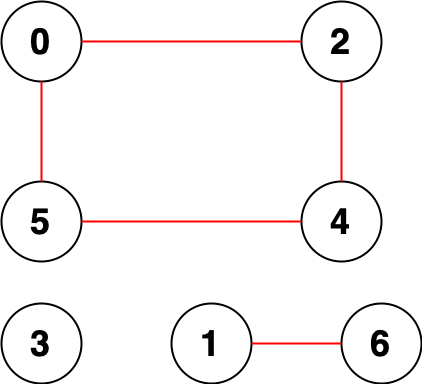
Input: n = 7, edges = [[0,2],[0,5],[2,4],[1,6],[5,4]]
Output: 14
Explanation: There are 14 pairs of nodes that are unreachable from each other:
[[0,1],[0,3],[0,6],[1,2],[1,3],[1,4],[1,5],[2,3],[2,6],[3,4],[3,5],[3,6],[4,6],[5,6]].
Therefore, we return 14.

 

Constraints:

• 1 <= n <= 105
• 0 <= edges.length <= 2 * 105
• edges[i].length == 2
• 0 <= ai, bi < n
• ai != bi
• There are no repeated edges.

C++ Code :

class Solution {

public:

typedef long long ll;

void dfs(int node, unordered_map<int,vector<int>>& m, ll& cnt, vector<int>& vis){

vis[node] = 1;

cnt++;

for(auto& i: m[node]){

if(vis[i]==0) dfs(i,m,cnt,vis);

}

}

long long countPairs(int n, vector<vector<int>>& edges) {

unordered_map<int,vector<int>> m; // making adjacency list

for(int i=0;i<edges.size();i++){

m[edges[i][0]].push_back(edges[i][1]);

m[edges[i][1]].push_back(edges[i][0]);

}

ll ans = ((ll)n*(n-1))/2;

vector<int> vis(n,0);

for(int i=0;i<n;i++){

if(vis[i]==0){

ll cnt = 0;

dfs(i,m,cnt,vis);

ans -= (cnt*(cnt-1))/2;

}

}

return ans;

}

};